Random Variables and its Probability Distributions

Suppose an instant lottery ticket is purchased for $\$2$. The possible prizes are $\$0, \$2, \$20, \$200$ and $\$1000$. Let $Z$ be the random variable representing the amount won on the ticket, and suppose $Z$ has the following distribution.

Determine $E\left(Z\right)$ and interpret its meaning.

The discrete random variable $X$ has the following probability distribution.

Determine the exact value of the mean of the distribution.

The discrete random variable k has probability distribution function given by $P(K=k)=\beta {(3-k)}^2$ for $k=0, 1, 2, 3, 4.$ Find the value of $\beta + E\left(k\right).$

Ten thousand $\mathrm{US}\$10$ lottery tickets are sold. One ticket wins a prize of $\mathrm{US}\$5000$, five tickets each win $\mathrm{US}\$1000$ , and ten tickets each win $\mathrm{US}\$200$. The price of ticket to make the lottery a fair game.

Ten thousand $\mathrm{US}\$10$ lottery tickets are sold. One ticket wins a prize of $\mathrm{US}\$5000$, five tickets each win $\mathrm{US}\$1000$ , and ten tickets each win $\mathrm{US}\$200$. Find the expected gain from one ticket.

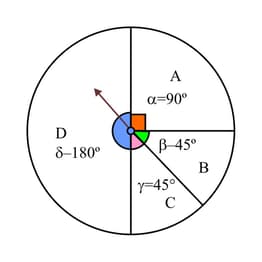
Alexandre is designing a game. A spinning arrow rotates and stops on one of the regions $A, B, C$ or $D$ as shown in the diagram.

Alexandre proposes the prizes shown in the table and that the game should cost $\mathrm{US}\$5$ to play.

Determine whether Alexandre's game is fair and justify your answer.

A handbag contains five coins and four keys and eight mints. Two items are taken out of the handbag one after the other and not replaced. Find the expected number of mints taken out of the handbag.

(Write answer in simplest fraction form)

A handbag contains seven coins and three keys. Two items are taken out of the handbag one after the other and not replaced. Find the expected number of keys taken out of the handbag.

(Write answer in simplest fraction form)

Sarah researches multiple births in a clinic, where she keeps records over a period of years of the genders of triplets born there. There are eight possible sequences of genders in a set of triplets, for example $\mathrm{MFM}$.

Assuming $\mathrm{P}\left(\mathrm{Male}\right)=\mathrm{P}\left(\mathrm{Female}\right)=0.5$, construct the probability distribution table of the random variable $\mathrm{M}=$the number of males born in a set of triplets.

Find the expected number of male births in a set of triplets. Interpret your result.

A probability distribution of random variable $\mathrm{X}$ is given by

Then the value of $\mathrm{E}(4\mathrm{x}+3)$ is

A player tosses two coins if two heads appears he wins Rs. $4,$ if one head appears he wins Rs. $2$, but if two tails appears he loses Rs. $3$. Find the expected sum of money he wins?

The p.d.f. of a continuous random variable $\mathrm{X}$ is given by $f\left(x\right)=\left\{\begin{array}{ll}\frac{x}{2},& 0<x<2\\ 0,& \text{ elsewhere }\end{array}\right.$. Then its mean is 

If the probability density function of a continuous random variable $\mathrm{X}$ is given by $\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{cc}\frac{\mathrm{k}(1-{\mathrm{x}}^2)}{4}& 0<\mathrm{x}<1\\ 0& \mathrm{elsewhere}\end{array}\right.$, then we get $\mathrm{E}(\mathrm{X}=\mathrm{x})=\frac{3}{k}$. Find the value of $k$.

A random variable $\mathrm{X}$ has the following probability distribution.

Then, $\mathrm{P}(1\le \mathrm{X}\le 4)$ is

If a continuous random variable $X$ has probability density function given by $f\left(x\right)=\{\begin{array}{cl}12A{x}^5,& 0<x<1\\ 0,& \text{otherwise}\end{array}$ then the value of $A$ is 

If $\mathrm{Var}\left(\mathrm{X}\right)=2$ then $\mathrm{E}\left(\mathrm{Var}\right(4\mathrm{X}+3\left)\right)=\mathrm{E}\left(32\right)$.

If the variance of a random variable $\mathrm{X}$ is $8$ and its mean is $2$ then the expectation of $X^2$ is 

In an entrance examination student has answered all the $120$ questions. Each question has $4$ options and only one option is correct. A student gets one mark for correct answer and looses $\frac{1}{2}$ marks for wrong answer. What is the expectation of a mark scored by a student if he chooses the answer to each question at random?

The following is a probability density function, $\mathrm{f}\left(\mathrm{x}\right)=5{\mathrm{x}}^4$ for$0<\mathrm{x}<1$.

A probability distribution of random variable $\mathrm{X}$ is given by

Find $\mathrm{E}(2\mathrm{x}+5)$.